Contents |
me339 - mechanics of the cell
| ellen kuhl - ekuhl.at.stanford.edu chris jacobs - christopher.jacobs.at.stanford.edu ron kwon - ronkwon.at.stanford.edu yufen shi - yufenshi.at.stanford.edu fall 2007 |
final project
zheng c, doll jc, gu e, hager-barnard e, huang z, kia aa, ortiz m, petzold b, shi y, suk sd, usui t, kwon r, jacobs c, kuhl e. exploring cellular tensegrity: physical modeling and computational simulation. proceedings of the ASME 2008 summer bioengineering conference 2008, marco island, florida. SBC2008-192407 (download).
cell design contest
design the stiffest and yet lightest cell! we will carry out simple tension and shear tests on your cell and determine its homogenized tension and shear stiffness. the stiffest and lightest cell will win. most creative designs will be awarded as well! and the winner is...
| 
| 
| 
|

| 
| 
| 
|
| 
| 
| 
|
goals
cells are the fundamental building blocks of life. the understanding of their characteristic biological features, their motility, their biochemistry and their interaction with the environment is crucial when cells are to be applied, modified or engineered in healthcare and modern medical therapies. this class focusses on the mechanical aspects of the cell which can be two fold: on the one hand, cell biology and biochemistry influence the mechanical properties of the cell. on the one hand the mechanical environment, load, pressure, stress or strain can influence the cell's shape and integrity, and eventually its biology and biochemistry. in the first part of this class, we will discuss how cell properties can be measured experimentally and how they can be characterized in the form of equations. concepts of energy and entropy will be elaborated for different structural units of the cell: the biopolymers, i.e., microtubules, actin and intermediate filaments and the biomembrane, i.e., the lipid bi-layer that forms the cell membrane. computational simulation tools will be introduced to explain and understand cell behavior in silico. in the second part, we address aspects of mechanotransduction which are part of active research in cell mechanics. we discuss different aspects of how cells sense loads and how signals are transmitted within the cell and through the extracellular matrix.
grading
- 30 % homework - 3 homework assignments, 10% each
- 30 % midterm - open notes, with calculators, no books
- 40 % project - oral presentations graded by the class, written part graded by us
syllabus
copyright ron kwon, ellen kuhl, chris jacobs, stanford, fall 2007
| day | date | topic | notes | ||
|---|---|---|---|---|---|
| tue | sep | 25 | introduction I - cell biology | s01 | jacobs |
| thu | sep | 27 | introduction II - cytoskeletal biology | s02 | kwon |
| tue | oct | 02 | introduction III - mechanics | s03 | kuhl |
| thu | oct | 04 | biopolymers I - bending & buckling | s04 | kuhl |
| tue | oct | 09 | first homework - biopolymers | h01 | solution |
| tue | oct | 09 | biopolymers II - statistical mechanics | s05 | kwon |
| thu | oct | 11 | biopolymers III - gaussian chain | s06 | kwon |
| tue | oct | 16 | biopolymers IV - freely jointed chain & wormlike chain | s07 | kwon |
| thu | oct | 18 | second homework - biopolymers | h02 | solution |
| thu | oct | 18 | cytoskeletal mechanics I - filopodia - fiber bundle model | s08 | kwon |
| tue | oct | 23 | cytoskeletal mechanics II - red blood cells - network models | s09 | kwon |
| thu | oct | 25 | biomembranes I - pipette aspiration | s10 | kwon |
| tue | oct | 30 | cytoskeletal mechanics III - muscle cells - tensegrity model | kuhl | |
| thu | oct | 01 | third homework - cytoskeleton | h03 | |
| thu | nov | 01 | biomembranes II - soap bubbles & cell membranes | s12 | kuhl |
| tue | nov | 06 | biomembranes III - tension, shear & bending | s13 | kuhl |
| thu | nov | 08 | mechanotransduction I | s14 | jacobs |
| tue | nov | 13 | mechanotransduction II | s15 | jacobs |
| thu | nov | 15 | midterm | m01 | |
| tue | nov | 27 | mechanotransduction III | s16 | jacobs |
| thu | nov | 29 | class projects - preparation, no class | ||
| tue | dec | 04 | class projects - oral presentations I | ||
| thu | dec | 06 | class projects - oral presentations II - winner design competition | d01 | kuhl |
| fri | dec | 14 | class projects - written projects due |
matlab files for cell design
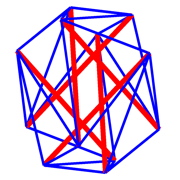
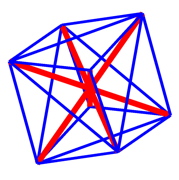
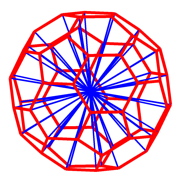
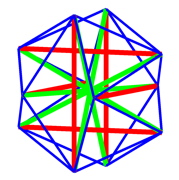
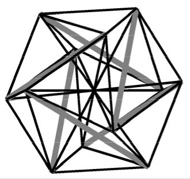
tensegrity structures have been known as architectual elements in structural design for a long time. due to the sophisticated structural interplay between compressive trusses tied together by tensile ropes they are super light weight structures with an incredible degree of stiffness and stability. a biological cell can be modeled as a tensegrity structure with microtubules as compressive elements and actin and intermediate filaments as prestressed tensile elements.

| 
| 
| 
|
the above tensegrity structures have been plotted with the matlab codes below. you might want to look at them as examples.
design_cell01.m ... the one we did in class
design_cell02.m ... the one without nucleus
design_cell03.m ... the one with nucleus
design_cell04.m ... the one with discretized nucleus
now design your own cell! use the above files as examples. define the nodel coordinates q0 and the element connectivity el. plot and describe your cell design!
matlab files for fe analysis of cells
now, if you wanted to see how your cell behaves when subjected to loading, you would have to download the finite element files below.
| 
| 
| 
| 
|
download the matlab nonlinear finite element code for the tensegrity cell
*now*
and you'll get a second one for your grandmother for free: matlab_cell.tar.gz !
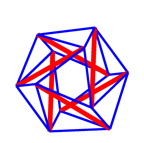
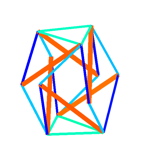
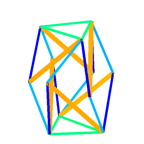
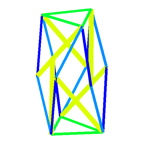
- start the finite element program by typing 'nlin_fem' into the matlab editor! you should see the undeformed cell structure on the left, the red trusses represent microtubules as compressive elements and the blue ropes represent the intermediate filaments as tensile elements.
- load the structure by typing 'step,,5' which applies a load to the three top nodes while the bottom nodes are fixed! you should see the sequence of configurations depicted above. in the matlab editor, you see the quadratic convergence of the newton method which is applied to solve the non linear finite element tensegrity equations.
- add an additional load by typing 'step,,10' and then unload by typing 'step,,-14'! check the characteristic features of tensegrity structures whose members rotate with respect to the vertical loading axis to stiffen the structure. the color code reflects the stress state of the elements, blue is tension, red is compression, compressive ropes are not depicted.
- try to do the same with the second input file by editing the 'nlin_fem.m' file and putting the % symbol in front of the 8th line rather than the 7th!
- modify the material parameters, the boundary conditions, the loading or the prestress by editing the input file! you will experience that the tensegrity cell structure is extremely sensitive to the prestress vs loading relation because its ropes will collapse in compression. the calculation fails because the structure loses integrity, the stiffness matrix is no longer invertible.
take a look @all the individual files you downloaded
i've tried to put comments to most of the variables, send me an email if you want moooore ;-)
nlin_fem.m ... the one and only
truss_03.m ... the one with the 3d truss and rope elements
inp_cell.m ... the cell input file with nucleus
inp_tens.m ... the cell input file without nucleus
extr_dof.m ... the one which extracts element information from the global
field
assm_sys.m ... the one with the strange big A operator
res_norm.m ... the one which tells you how far you are away from your ultimate goal
solve_nr.m ... the one with the solution to all problems
col_maps.m ... the one with all the colors
plot_mat.m ... the one to plot the undeformed configuration
plot_spa.m ... the one to plot the deformed configuration with stresses
additional reading
(1) boal d: mechanics of the cell, cambridge university press, cambridge, 2002
(2) howard j: mechanics of motor proteins and the cytoskeleton, sinauer associates, sunderland, 2001
(3) alberts b et al.: molecular biology of the cell, garland science, taylor & francis, new york, 2002